You know the classic question:

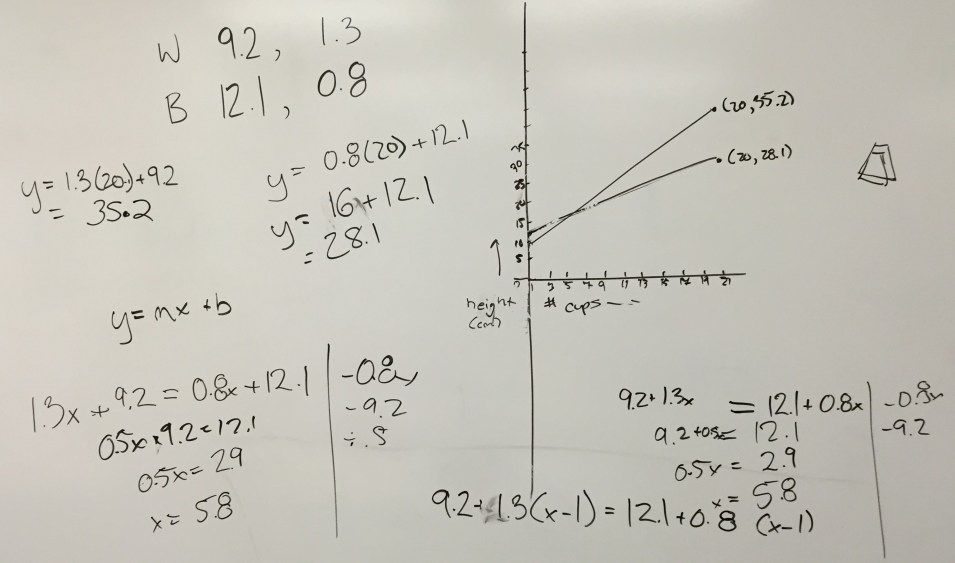
You have 832 ft of fencing and you want to build a rectangular pen along side a river with maximum area. 

Well, as we know, the textbook approach to this is generally to create a length and width equation, use it to create an area function, and find the maximum value of this function.

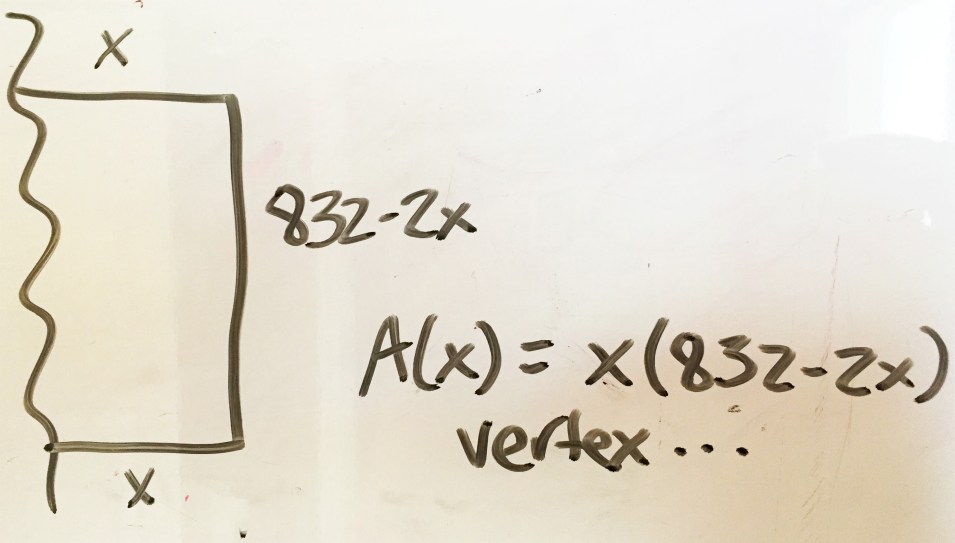
Depending on how you go about it, it gets a bit thick on the calculations, and most students require a calculator for it. They can learn the procedure though and it works for them.

HOWEVER,  I had a student come up to me after a class where I asked them to find the dimensions of a patio we could build with a given number of feet of fencing outside our classroom so that we have the maximum area possible. He told me that he thinks he has noticed a pattern within these problems where there is a 2:1 ratio between the sides for a maximum area.

My gut instinct was to introduce doubt, but encourage him to continue pursuing this idea. I told him about how mathematicians will notice things they think may always be true, and then find ways to prove or disprove their conjectures. I also told him that one way to easily disprove it is by finding a counterexample. So I set him on his way telling him to try many examples and see if his idea ever fails.

He had shared a few attempts at explaining his rationale with me, but they were not convincing. I wasn’t sure if he’d pursue it further or not, but I left it at that.

About two weeks later, which was last night, this question was on a quiz. This student, along with another student, were chatting after class . . . because they just can’t get enough of math class . . . and were discussing the farmer’s-pen-by-the-river problem. They are both very engaged and creative students who are both very strong thinkers. But the contrast in approaches was interesting to observe.

One student asked the other about how they approached this problem, and the student who had spent all this time thinking about his conjecture didn’t remember what he got on the problem. So the other student reminded him of what the problem was, and went on to explain the classic solution approach of using the vertex of the area function to find the maximum value for the length of the pen. The other student smiled, and said, “why do all that work when you can do this . . .” and he showed the following:

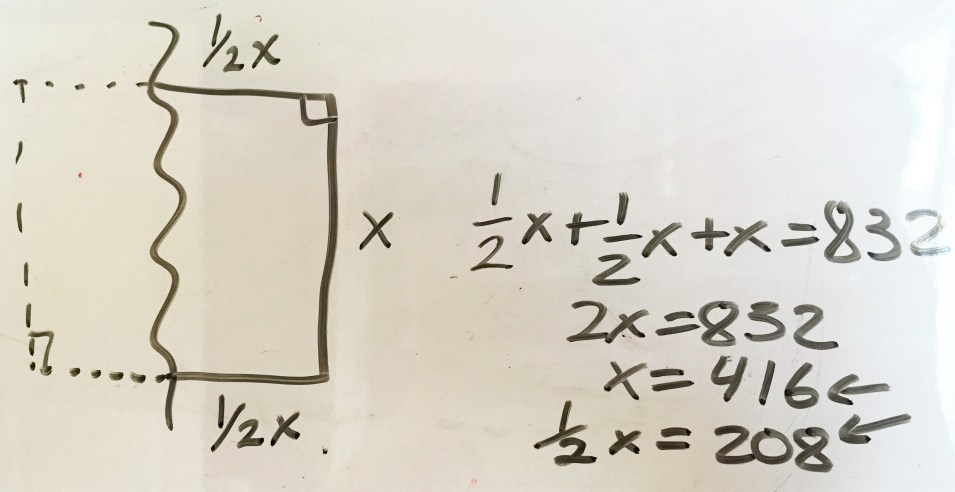
The part that blew me away was his reasoning:

HE EXTENDED THE RECTANGLE INTO A SQUARE!

Way to think out of the “box” . . . pun intended – lol.

By claiming that the area is maximized when something is a square, and that the pen problem is really always half a square, the proportions can be used to quickly deduce the length and width.

And even at this point, I continued my doubt. I told him that this is a very elegant and creative idea, and it clearly gives the right answer in this case, but that he should further work on how to convince someone that this is always the case.

What impressed me the most is that the doubt that I provided early on somehow motivated the student to refine his thinking.

I know for sure that without all of the work on building a classroom culture of thinking and communicating, this would not have happened in this way. Without random groups, these students would not be working together, commuting to class together, pursuing the next math class together, and discussing Greek Philosophy together after class (true story, they actually were)!

Opening up communication and visibility of thinking in class is so important. I am finding this idea being supported within the work of my colleagues. The other day, one of my colleagues told me she notices a big difference in student thinking when she has a classroom where students can work on whiteboards around the room. Another colleague also recently shared with me that she notices a huge difference in student participation with each other in a lecture based university level math course when she takes the time to implement a social activity during the first class. We really need more SOCIAL in the university learning context.